Gemiddeld genomen
Wordt het gemiddelde vaak verkeerd gebruikt
Gemiddelden worden dagdagelijks in het nieuws genoemd en in radio- of Tv-programma’s besproken.
Ook binnen spoedzorg organisaties is “het gemiddelde” een veel gebruikte statistiek in rapportages en gesprekken. Zo worden indicatoren regelmatig bekeken als gemiddelden over een periode.
Dit gebeurt omdat bijna iedereen het gemiddelde kent. Het gemiddelde is naast een percentage en het absolute aantal één van de “go-to” statistieken om data inzichtelijk te maken.
Je telt alle waardes op en je deelt het vervolgens door het aantal observaties. Et voilà, je hebt je gemiddelde. Simpel en doeltreffend.
Misschien denk je: “joh, iedereen begrijpt toch wel een gemiddelde?”
Toch zit het mij dwars hoe vaak het gemiddelde gebruikt wordt als antwoord op vragen die het gemiddelde niet (in z’n eentje) kan beantwoorden.
Het gemiddelde geeft in een beperkt inzicht in datgene dat je eigenlijk wil weten in veel gevallen. Er zijn een aantal belangrijke eigenschappen die je altijd samen met het gemiddelde wil zien.
Het is namelijk belangrijk om te weten over hoeveel observaties het gemiddelde is berekend en hoe ver de waarden uit elkaar liggen.
Een voorbeeld
Een kind haalt op school een gemiddeld cijfer van een 5,5.
Alleen op basis van het gemiddelde weet je nu eigenlijk niet voldoende om te bepalen hoe je het kind kan helpen het cijfer te verbeteren.
Een 1 en een 10 hebben een gemiddelde van 5,5. Een 5 en 6 hebben dat zelfde gemiddelde van 5,5. Kijk je in dit geval alleen naar het gemiddelde kan je zomaar de verkeerde oplossing pakken.
Het is dus altijd belangrijk altijd de onderstaande vragen te stellen bij het zien van een gemiddelde:

1. Hoe ver liggen de observaties af van het gemiddelde?
In de statistiek wordt deze spreiding vaak berekend als de standaarddeviatie. Dit geeft cruciale informatie, maar ontbreekt erg vaak in berichtgeving en verslaglegging. De standaarddeviatie geeft inzicht in de opbouw van het gemiddelde.
Als we even teruggaan naar het voorbeeld van de scholier, dan hoort bij een cijferlijst van een 1 en een 10 een standaarddeviatie van 4,5 en bij de cijferlijst van 5 en 6 eentje van 0,5.
In een oogopslag wordt hier duidelijk dat in het eerste geval de scholier zowel hele hoge als hele lage cijfers haalt, terwijl de scholier in het tweede geval middelmatig scoort.
Wanneer je alleen naar het gemiddelde kijkt, dan zit die informatie nog verstopt. Met de standaarddeviatie kan je deze informatie inzichtelijk maken.
De standaarddeviatie is wat lastiger om te bepalen dan het gemiddelde. Naar mijn idee wordt deze dus daarom vaak achterwege gelaten. Je berekent een standaard deviatie
- Bereken de afwijking van iedere waarde tot het gemiddelde
- Kwadrateer deze afwijkingen.
- Deel de som van deze gekwadrateerde afwijkingen door het aantal observaties minus één (nu heb je de “variantie” berekend)
- Neem de wortel van de variantie om de standaarddeviatie te krijgen.
Wees gerust, je kan het makkelijk in bijvoorbeeld Excel of met verschillende online tooltjes berekenen.
2. Hoe groot is de groep observaties waarop het gemiddelde is gebaseerd?
Verder is het erg belangrijk om te kijken naar de grootte van de groep observaties waar het gemiddelde op gebaseerd is.
Kijk je bijvoorbeeld naar een heel klein aantal schoolcijfers, dan kan het gemiddelde en ook de standaarddeviatie vertekenen.
De mate van toeval en geluk spelen een aanzienlijke rol in kleine “populaties”. Heb je meer observaties, dan wordt het gemiddelde meer robuust als indicator om naar te kijken.
3. Wat is de modus en hoe verhoudt deze zich tot het gemiddelde?
Soms is zelfs het gemiddelde met standaarddeviatie en groepsgrootte niet voldoende voor een compleet beeld.
Wanneer je bijvoorbeeld het inkomen van inwoners van een land wil vergelijken. In dat geval is het slim om ook te kijken naar het meest voorkomende (modale) inkomen.
Het gemiddelde inkomen zal namelijk behoorlijk hoger liggen en een verkeerd beeld geven.
Dit plaatje uit 2018 van het CBS laat het goed zien:
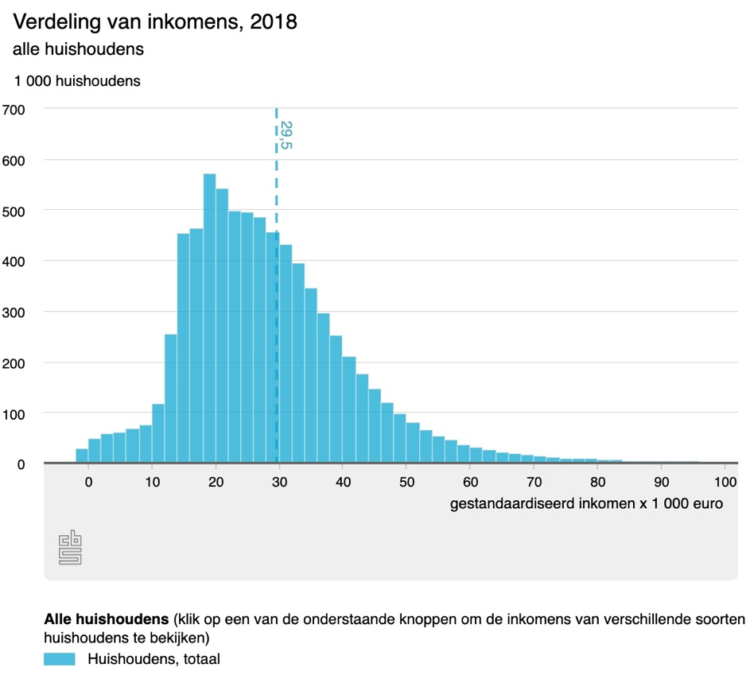
De stippellijn is het gemiddelde inkomen, maar dat gemiddelde wordt omhoog getrokken door een aantal gelukkigen met hoge inkomens. De meest voorkomende waardes, de modus, liggen een stuk meer naar links, bij het hoogste staafje van 18.000 euro.
Tot slot
Het gemiddelde is op zich geen slechte statistiek. Het geeft een beeld over de algemene tendens van meerdere observaties .
Echter, vaak wordt de standaarddeviatie en groepsgrootte vergeten.
Dat leidt tot ontbrekende informatie. Ben je je daar niet bewust van, kan dit zorgen voor onbedoeld verkeerde conclusies.
Het mooie van statistiek is dat het in complexe situaties dezelfde regels heeft als in hele overzichtelijke simpele situaties.
Toch lijkt de begripsvorming van het gemiddelde in de ene situatie helderder dan in de andere.
Wanneer je een gemiddelde ziet, vraag jezelf dan altijd af in welke context dit gemiddelde tot stand gekomen is.
Na het lezen van dit artikel kan je met een gerust hart een artikeltje lezen over de stijging van de gemiddelde huizenprijzen en concluderen dat het maar weinig zegt. Er is namelijk veel te veel onduidelijkheid over de totstandkoming van dit gemiddelde.
__
afbeelding 1 via Unsplash
afbeelding 2 via CBS




